Is Silver Medal Deserved in Single-Elimination Tournament?
#algorithm Motivation
In single-elimination tournament, a team is immediately eliminated when they lose a game. This means if a team is the actual second best, they could be eliminated early in the game by the very best team if they were unlucky, and thus not reach the final to get the silver medal. Conversely, the team who did get the silver medal might not deserve it because they did not prove to be better than all other teams.
So this blog post attempts to answer, to what extent is the silver medal deserved by merit rather than by luck?
Two Concrete Questions, Same Answer
The question above is actually deceptively ambiguous, and can be reformulated in one of the two concrete forms:
- If we know a team won silver medal, what is the probability that they are actually the second best in the tournament?
- If a team is the second best in the tournament, what chance does it have to win the silver medal?
Interestingly (or perhaps intuitively), the answers to these two questions are the same. In a tournament of $N$ teams (assume $N$ is 2 to an integer power for simplicity), the answer to both questions is $\frac{N}{2(N-1)}$, which is close to 50% especially when $N$ gets large (for example, when $N=32$, the chance is 51.6%). I only realize this “coincidence” after doing the calculation, but there must be a simpler explanation why they are the same.
For illustration purpose, we will assume $N=8$ for the rest of this blog post, but the reasoning applies to general $N$ as well. The diagram below shows 8 teams, $a, b, c, d, e, f, g, h$. In this tournament, team $a$ wins the gold medal, and team $e$ wins the silver.
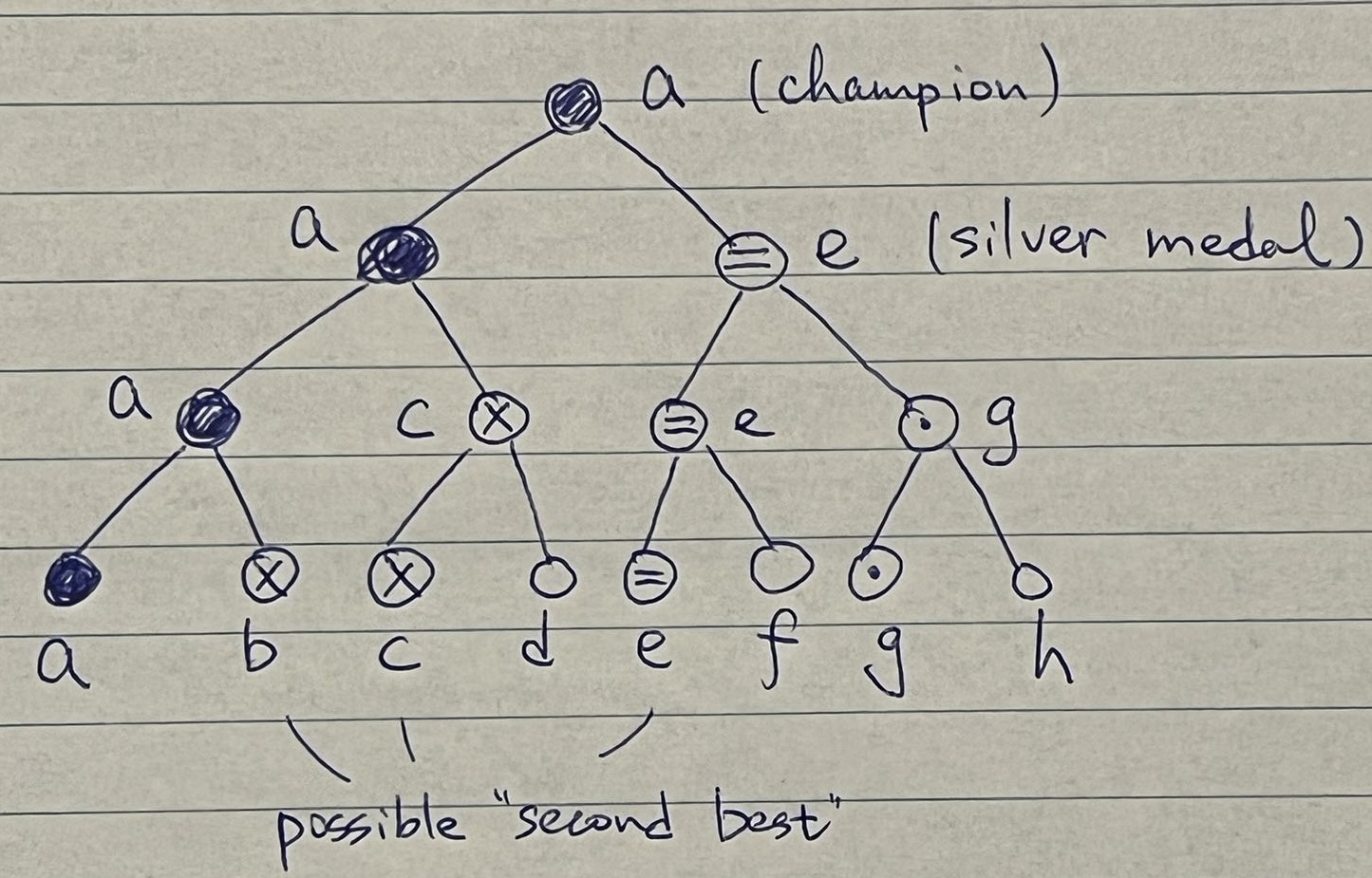
$P(e\textrm{ is second best} | e\textrm{ wins silver medal})$
Given the outcome of the game as shown above, we know possible 2nd best teams are $b$, $c$ and $e$, because they have only been defeated by team $a$, the gold medalist, but no one else. In this section, we will compute the chance for each of them being the second best given the outcome of this tournament.
In order to compute this posterior probability, we will count number of valid permutations in each case.
- By permutation, we mean an order assignment to the teams, e.g. $(a,b,c,d,e,f,g,h)=(1,2,3,4,5,6,7,8)$, where smaller number means the team is better.
- By valid permutation, we mean the order should be consistent with the outcome of the game. For example, $(a,b,c,d,e,f,g,h)=(1,2,3,4,5,6,7,8)$ or $(a,b,c,d,e,f,g,h)=(1,5,3,4,2,6,7,8)$ are valid permutations, while $(a,b,c,d,e,f,g,h)=(2,1,3,4,5,6,7,8)$ is not (because $a$ beats $b$ so its number should be smaller).
We denote number of valid permutation of certain condition as $N_\textrm{valid}(\textrm{condition})$, and the answer to this question is therefore
\[P(e\textrm{ is second best} | e\textrm{ wins silver medal}) = \frac{N_\textrm{valid}(e\textrm{ is second best})}{N_\textrm{valid}(b\textrm{ is second best}) + N_\textrm{valid}(c\textrm{ is second best}) + N_\textrm{valid}(e\textrm{ is second best})}\]Now we will compute each term in the equation:
- For $N_\textrm{valid}(b\textrm{ is second best})$, we need to permute $c,d,e,f,g,h$ with $3,4,5,6,7,8$. If there isn’t any constraint, there will be $6!=720$ permutations. It can be shown that each game will eliminate half of the permutations (e.g. $c$ beats $d$, so $c<d$, i.e. we eliminate all permutations where $c>d$). More importantly, in single-elimination tournament, all those eliminations are independent (the relationship between $c$ and $d$ does not affect that of $e$ and $f$). Therefore, $N_\textrm{valid}(b\textrm{ is second best})=6!/2^4$ because there are 4 relevant elimination games ($c$ vs $d$, $e$ vs $f$, $g$ vs $h$, $e$ vs $g$).
- For $N_\textrm{valid}(c\textrm{ is second best})$, we use the same logic, but there are only 3 relevant elimination games – $c$ vs $d$ is no longer relevant since we already know $c$ is the second best in the condition. Therefore $N_\textrm{valid}(c\textrm{ is second best})=6!/2^3$.
- Finally, for $N_\textrm{valid}(e\textrm{ is second best})$, only 2 games $c$ vs $d$ and $g$ vs $h$ are relevant, so we get $N_\textrm{valid}(c\textrm{ is second best})=6!/2^2$.
Putting everything together, we have
\[P(e\textrm{ is second best} | e\textrm{ wins silver medal}) = \frac{6!/2^2}{6!/2^4 + 6!/2^3 + 6!/2^2} = \frac{2^2}{1+2^1+2^2} = \frac{4}{7}\]$P(x\textrm{ wins silver medal} | x\textrm{ is second best})$
This turns out to be an easier question. If we know $x$ is the second best, in order for them to win the silver medal, they just need to be lucky enough to not meet $a$ until the final game. In other word, it needs to be assigned to one of the $e,f,g,h$ position, not $b,c,d$ (it cannot be assigned to $a$’s position because $a$ is the gold medalist, not silver). Therefore $x$’s chance of winning silver medal is also $4/7$ (4 “lucky” positions out of 7 possible ones).