Transformer / GPT Notes
#ai #gpt #transformer We consider a decoder-only architecture for now, and refer to it as “the decoder” (we could also call it the transformer or the GPT).
Input, Output, and Context Length
The decoder takes in $I$ tokens, and outputs one token at a time until the <END> token is generated. In other words,
it will generate $O$ tokens, but the number $O$ is decided by the model itself. The decoder has a preset context length
$L$ (a.k.a. block size), and it has to be bigger than the input and output combined, i.e. $L \geq I + O$.
Since the generation is done by one token at a time, the total decoding time is (roughly) proportional to number of output tokens $O$.
- Conceptually, the decoding complexity is really $I + (I+1) + \cdots + (I+O-1)$, because at $o$-th step, we only need
to run the forward pass on $I+(o-1)$ tokens.
- However, since the decoding is implemented with matrix multiplication with masking, we might need to pay the full
cost $L$ for each token.
- With that said, it seems foolish to run the full pass of $L$ when $I+(o-1)$ is very small, so I imagine there could be some optimization, using one scheme when $I+(o-1)$ is in $[128, 256)$, and another for $[256, 512)$, etc.
- However, since the decoding is implemented with matrix multiplication with masking, we might need to pay the full
cost $L$ for each token.
On the other hand, we note that the model size is independent of context length $L$. In other words, to support larger context length, we need to pay more cost at decoding time, but not necessarily a larger model.
Size of the Model
We used the table from GPT3 paper below to infer the relationship between model size and various dimensions.
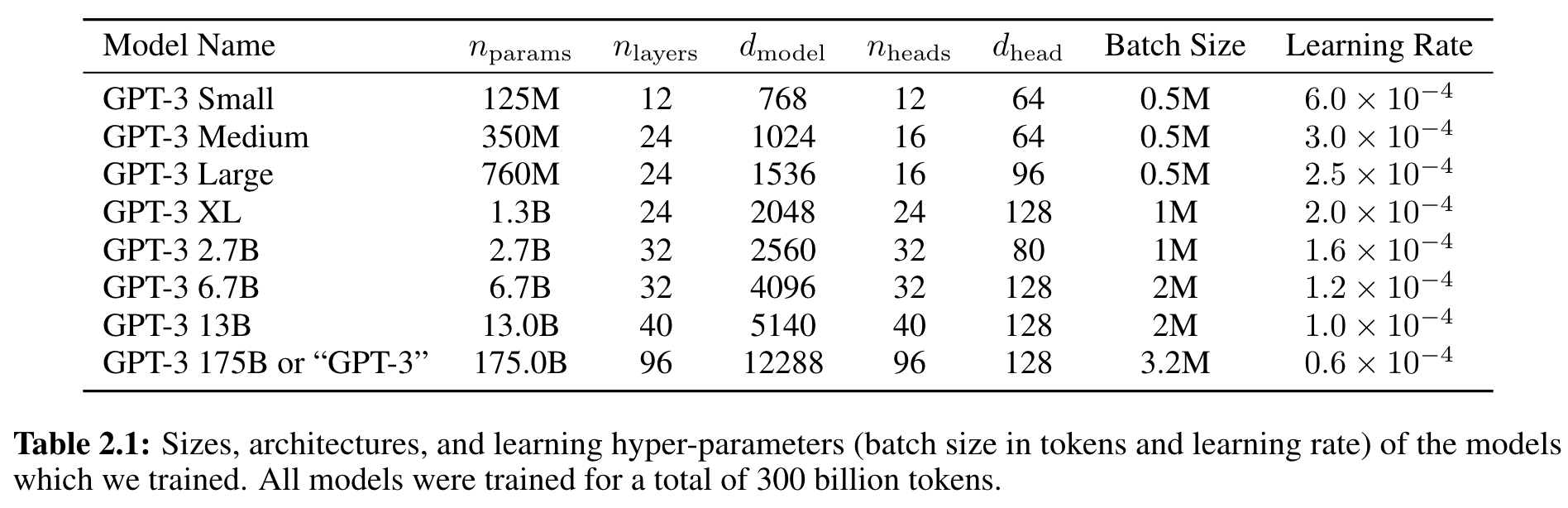
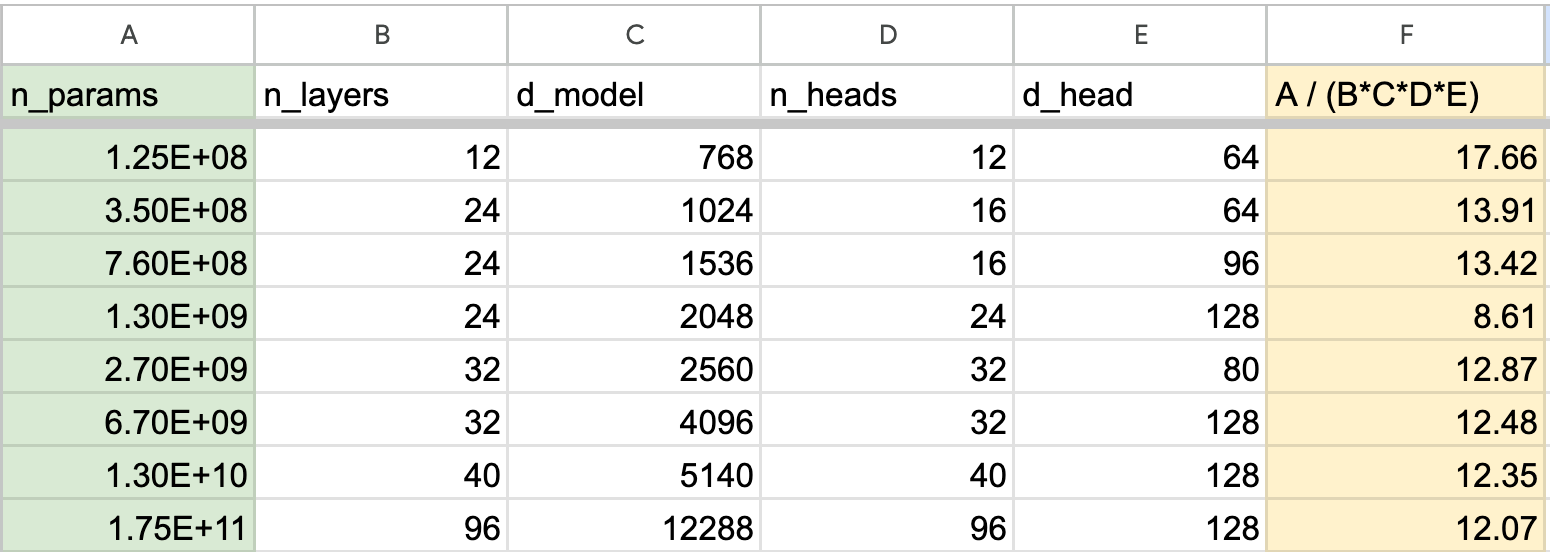
From the fiting below, we see that the size of the model is roughly proportional to the following dimensions:
- $n_\textrm{layers}$: the number of transformer layers (blocks)
- $d_\textrm{model}$: the dimension of the model, i.e. the word embedding dimension
- $n_\textrm{heads}$: the number of attention heads
- $d_\textrm{head}$: the dimension of each attention head
References
- [The Transformer Paper] Ashish Vaswani et al. Attention Is All You Need. https://arxiv.org/abs/1706.03762
- [GPT3 Paper] Tom B. Brown. Language Models are Few-Shot Learners. https://arxiv.org/abs/2005.14165
- Andrej Karpathy. Let’s build GPT: from scratch, in code, spelled out. https://www.youtube.com/watch?v=kCc8FmEb1nY